
[Photo by João Silas on Unsplash](https://s3-us-west-2.amazonaws.com/secure.notion-static.com/8fd117c1-ca90-4d86-a025-e0a8d3380252/0JK-LugSqR7swgnBI)
Photo by João Silas on Unsplash
In this article, we’ll explore a state-of-the-art method of machine learning interpretability and adapt it to multivariate time series data, a use case which it wasn’t previously prepared to work on. You’ll find explanations to core concepts, on what they are and how they work, followed by examples. We’ll also address the main ideas behind the proposed solution, as well as a suggested visualization of instance importance.
It’s not just hype anymore, machine learning is becoming an important part of our lives. Sure, there aren’t any sentient machines nor Scarlett Johansson ear lovers (shoutout to Her) out there, but the evolution of these algorithms is undeniable. They can ride cars, assist in medical prognosis, predict stock, play videogames at a pro level and even generate melodies or images! But these machine learning models aren’t flawless nor foolproof. They can even be misleading, showing an incorrect probability in a sample that is very different from the training data (I recommend having a look at Christian Perone’s presentation addressing uncertainty [1]). Thus, especially in critical applications such as in diagnosing a patient or deciding a company’s strategy, it’s important to at least have some understanding of how the model got to its output value so that users can confirm if it’s trustable or not. Furthermore, in the case of a high-performance model coupled with an adequate interpretation, it can lead to surprising revelations, such as the impact of a gene in the diagnosis of a disease or a certain time of the year on sales.

We are not quite there yet in AI. GIF by the awesome Simone Giertz.
So it’s a no-brainer to apply interpretability techniques on all that is machine learning, right? Well, more or less. While simpler models like linear regression and decision trees are straightforward to analyze, more complex models such as a neural network aren’t self-explanatory, particularly in scenarios of high dimensionality of data and parameters. Some architecture changes have been suggested to make neural networks easier to interpret, such as attention weights. However, not only do these approaches require increasing the number of parameters and altering the model’s behavior (which could worsen its performance), they may not give us the full picture (attention weights only indicate the relative importance of each feature, not if it impacted the output positively or negatively). As such, there has been this tradeoff between performance and interpretability, where in order to be able to interpret the model, it would have to be simple enough or specially adapted in some way, restricting its potential.
Fortunately, research has been growing on perturbation-based methods, a family of interpretability techniques that apply changes in the input data (i.e. perturbations) to calculate importance scores, usually without requiring a specific model architecture. This means that these methods can be model-agnostic, making every possible model interpretable and with that eliminating the performance/interpretability tradeoff (albeit with some caveats that we’ll address later). So, let’s go through some of the main concepts behind modern perturbation-based interpretability techniques.
Shapley values are a concept from game theory, first introduced by Lloyd Shapley in 1953 (I know that I said “modern”, but bear with me here), which defined a way to calculate each player’s contribution in a cooperative game. It all comes down to a single equation. Consider a total of N players, i the player whose contribution we’re calculating, φi player i’s contribution, S a subset of players excluding i (with |S| meaning the number of players in subset S) and v the function that outputs the total payoff for the set of input players. To calculate player i’s contribution, we calculate the following equation:

Shapley values equation.
In other words, each player’s contribution is determined by the weighted average of that player’s marginal contributions, over all possible combinations of players. Note that by combination I mean a subset of players in the game, regardless of their order, and by marginal contribution I mean how the payoff changes when that specific player joins in, in the current combination. Now that we understood the marginal contribution part, there’s still that messy stuff on the left. These seemingly complex weights can actually give rise to a simple equivalent version of the Shapley values equation:
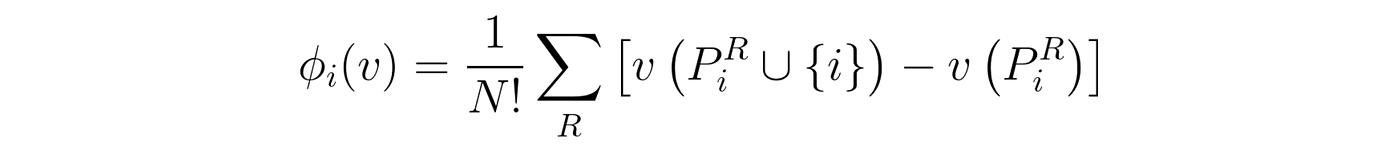
Equivalent Shapley values equation.
In this equation, we iterate through all possible permutations (R) of the full list of players, instead of just using the unique marginal contributions. Note that by permutation I mean the order in which players are added (e.g. player 1 starts the game, then player 2 joins in, followed by player 3, etc). In this case, it now has the symbol PiR (sorry, can’t really write in equation form in Medium text), which represents all the players that appeared before i, in the current order R. This equivalence means that the weights are set in a way that takes into account how many times a unique marginal contribution appears, on all possible orders of the players. Moreover, it’s the way those weights are defined that allow Shapley values to fulfill a set of properties that ensure a fair and truthful distribution of contributions throughout the players. In order to keep this post reasonably short, I’m not going to list them here, but you can check Christoph Molnar’s Interpretable Machine Learning book [2] if you want to know more.
To illustrate this, as a football fan, imagine the following scenario:
Imagine we have three strikers (i.e. players that play forward in the field, with the main objective to score or assist in as many goals as possible). Let’s call them B, L, and V. Let G be the function that, for a set of strikers in play, outputs how many goals are scored by the team. With that in mind, imagine that we have the following goals scored when each set of players are on the field:

Think that in this game all players will eventually be playing, it’s just a matter of when each one goes in (beginning on the starting squad or joining in the first or second substitution). As such, we have 6 possible scenarios of them getting in the game, to which we need to calculate marginal contributions: